
Gaferra
Author’s Note
The simulation was conducted in conjunction with a simulation of U.S. Treasury yields, reflecting the correlations between the 12 factors driving yields in each country. For more information about the U.S. Treasury simulation, please contact the authors.Both The simulation of German foreign debt and U.S. government bond yields will affect foreign exchange rates, resulting in the following distribution of the euro-dollar exchange rate one year later:
SAS Institute Inc.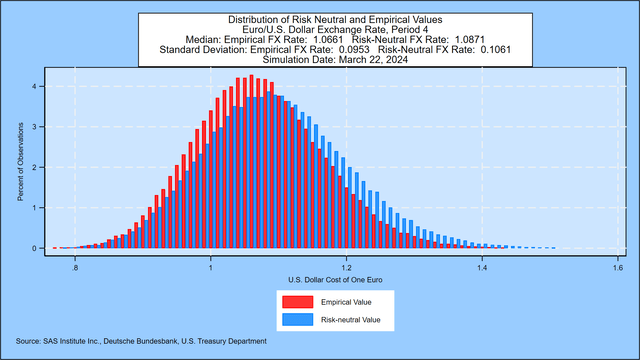
This week’s foreign debt yield simulation
As explained in Professor Robert Jarrow’s book cited below, forward rates contain a higher risk premium than the market expects for 3-month forward rates.We document the size of this risk premium in the chart below, which shows the zero-coupon yield curve implied by current German bund prices compared to the annualized compound yield expected by market participants on 3-month Treasuries Expectations are based on daily changes in government bond yields for 14 countries since 1962. The risk premium (return on long-term investing) is moderately positive and remains so over the entire term to 30 years. The chart also shows the steady decline in yields over the previous seven years, as discussed below.
SAS Institute Inc.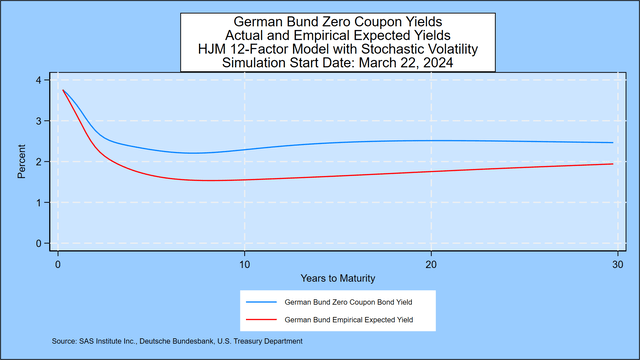
For more information on this topic, see the analysis of government bond yields for 14 countries as of January 31, 2024 in the appendix.
Yield inversion, negative interest rates and the chances of German Bunds over the next 10 years
In this week’s Eurozone forecast, the focus is on three elements of interest rate behavior: the future probability of an inversion of the yield curve predicting a recession, the probability of negative interest rates, and the probability distribution of German Bund yields over the next ten years.
We start with the German Bund closing yield curve published daily by the Deutsche Bundesbank and other sources. Using the maximum smoothness forward rate method, Friday’s implied forward rate curve showed a rapid rise in 1-month rates to an initial peak of 3.72%, compared with 3.63% two weeks ago. After the initial rise, there was some volatility until the rate peaked again at 2.85% (up from 2.77% two weeks ago) before falling to a lower level of 2.29% at the end of the 30s, up from 2.46% two weeks ago. year horizon.
SAS Institute Inc.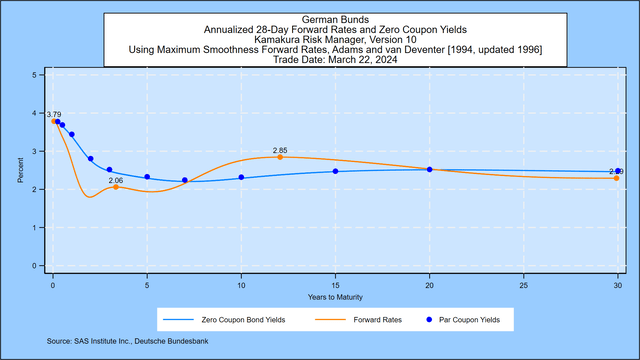
Using the methodology outlined in the appendix, we simulated 100,000 future paths of the German Bund yield curve over 30 years. The next three sections summarize the conclusions we draw from our simulations.
Inverted Bund Yield: Now inverted, the probability by September 20, 2024 is 66.9%
Many economists have concluded that a downward sloping yield curve is a strong indicator of a future recession.A recent example is this paper Alex Domarsh and Lawrence H. Summers.
We measure the probability that the 10-year par bond yield is lower than the 2-year par bond yield in each scenario during the first 80 quarters of the simulation.(1) The chart below shows that the chance of a yield inversion reached 66.9% during the 91-day quarter ending September 20, 2024, compared with 65.4% two weeks ago.
SAS Institute Inc.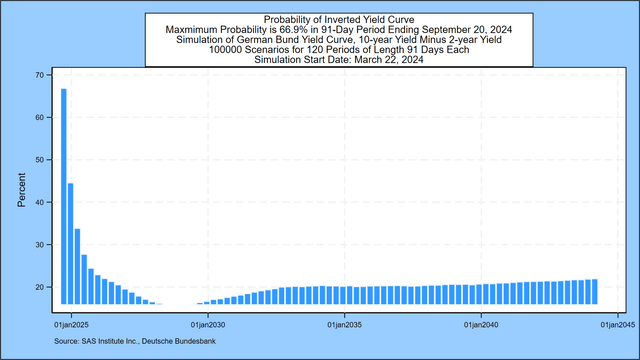
3-month negative yield: By December 14, 2029, the probability is 21.9%
The chart below depicts the probability of negative bill rates for all 3 months of the next 3 decades except the first 3 months. The chance of negative interest rates for the period ending December 14, 2029, started out close to zero but peaked at 21.9%, compared with 22.2% two weeks ago.
SAS Institute Inc.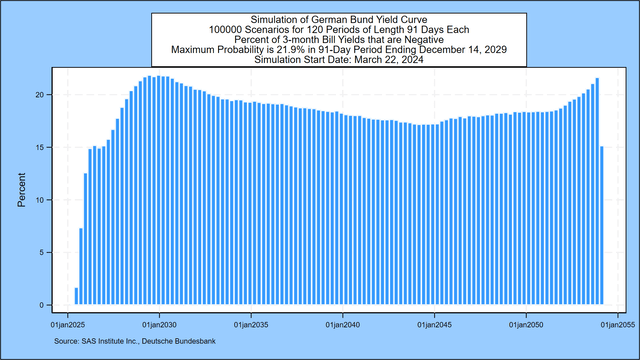
Calculate the default risk caused by interest rate maturity mismatch
In light of the interest rate risk-driven collapse of Silicon Valley Bank in the US on March 10, 2023, we have added a table that also applies to mismatches in long-term bond purchases by banks, institutional investors, and individual investors. German Bunds Borrow Short-Term Funds. We assume that the only asset is a 10-year German Bund purchased at time zero with a par value of €100. We analyze default risk for four different ratios of initial market value of equity to market value of assets: 5%, 10%, 15% and 20%. For the banking example, we assume that the only liability category is deposits that can be withdrawn at face value at any time. In the case of institutional and retail investors, we assume the liability is essentially a margin borrowing/repurchase agreement with the potential for margin calls. For all investors, the liability amount (95, 90, 85, or 80) represents the “strike price” of the put option held by the liability holder. When the value of assets falls below the value of liabilities, insolvency can result through margin calls, bank runs, or regulatory takeovers (in the case of the banking industry).
The chart below shows the cumulative 10-year probability of failure for each of the 4 possible capital ratios when the asset maturity is 10 years. For the 5% scenario, the probability of default is 43.77%, a change from 43.80% two weeks ago.
SAS Institute Inc.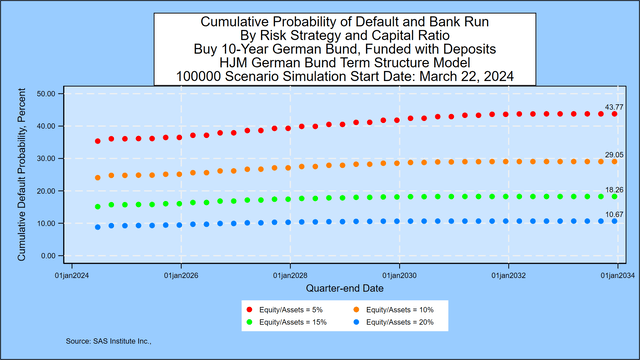
This default probability analysis is updated weekly based on the German bund yield simulation described in the next section. The calculation process is the same for any portfolio of assets that contains credit risk.
German Bund Yield Probability in the Next 10 Years
In this section, the focus turns to the next decade. This week’s simulation shows that the most likely range for the three-month bill yield in the Bund market in ten years is 0% to 1%, the same as two weeks ago. The chance of the 3-month yield falling within this range is 26.64%, compared with 26.45% two weeks ago. Note the downward shift in the second and third half-year periods. The most likely range for the 10-year German Bund yield is 1% to 2%, also unchanged from two weeks ago. The chance of being in that range is 22.32%, compared with 22.21% two weeks ago.
In a recent article on Seeking Alpha, we pointed out that predicting “heads” or “tails” when flipping a coin misses critical information. What experienced bettors need to know is that on average, for a fair coin, the chance of heads is 50%. For investors, the prediction that the next coin toss will be “heads” is effectively worthless because the outcome is purely random.
The same goes for interest rates.
In this section, we use a half-year time step to present the detailed probability distributions of the 3-month bill rate and the 10-year foreign debt yield.(2). We give the probability of each time step rate in the form of 1% “rate buckets”. The forecast for the return on the 3-month note is shown below:
SAS Institute Inc.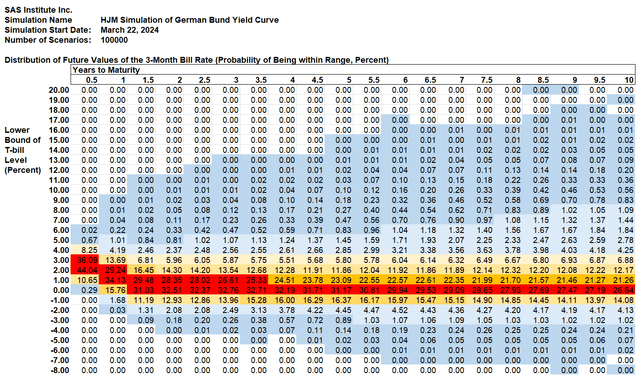
3-month bill yield data:
SASDEU3m20240322.xlsx
Column 4 shows the probability that the 3-month note will yield between 1% and 2% in 2 years: 28.35%. The probability that the 3-month yield will be negative within 2 years (which is often the case in Europe and Japan) is 12.93% plus 2.08% plus 0.18% plus 0.00% = 15.19% (difference due to rounding). Cells shaded blue represent a positive chance of occurrence, but the chance has been rounded to the nearest 0.01%. The shading scheme works as follows:
- Dark blue: probability greater than 0% but less than 1%
- Light blue: The probability is greater than or equal to 1% and less than 5%
- Light yellow: The probability is greater than or equal to 5% and 10%
- Medium yellow: The probability is greater than or equal to 10% and less than 20%
- Orange: The probability is greater than or equal to 20% and less than 25%
- Red: The probability is greater than 25%.
The chart below shows the same odds for the 10-year German Bund yield derived as part of the same simulation.
SAS Institute Inc.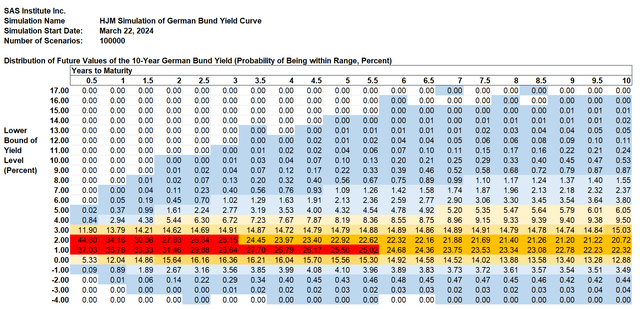
German ten-year government bond yield data:
SASDEU10y20240322.xlsx
Appendix: Bund rate of return simulation method
Probabilities are derived using the same method recommended by SAS Institute Inc. for its KRIS® Kamakura Risk Manager® client. A moderate technical explanation is given later in the appendix, but we first summarize it briefly.
Step one: we take Foreign debt closing yield curve as our starting point.
Step 2: We use the point on the yield curve that best explains the changes in the historical yield curve. We notice in the chart below that the span of foreign debt yields (in terms of interest rate levels and maturities) is only 40.69% of the historical experience of 14 countries:
SAS Institute Inc.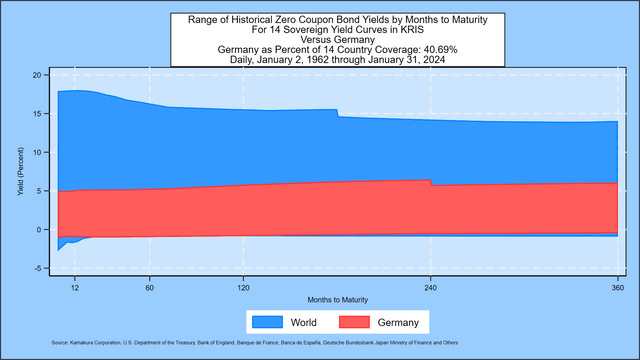
To achieve the highest level of realism in prospective simulations, the use of international databases is crucial. Using daily government bond yield data for 14 countries from 1962 to January 31, 2024, we concluded that 12 “factors” drive nearly all changes in government bond yields. The countries on which the analysis is based include Australia, Canada, France, Germany, Italy, Japan, and New Zealand. Russia, Singapore, Spain, Sweden, Thailand, United Kingdom and United States of America. Data from Russia is not included after January 2022.
Step 3: We measure the volatility of changes in these factors and the change in volatility over the same period.
Step 4: Using these measured volatilities, we generate 100,000 random shocks at each time step and derive the final yield curve.
Step 5: We “validate” the model to ensure that the simulation accurately prices the starting Bund curve and is as historically accurate as possible. The method for doing this is described below.
Step 6: We take all 100,000 simulated yield curves and calculate the probability that the yield falls in each 1% “bucket” shown on the chart.
Do nominal yields accurately reflect expected future inflation?
We noted in a recent article on Seeking Alpha that, on average, investors buying long-term bonds almost always perform better than rolling U.S. Treasury bills. This means that market participants usually, but not always, accurately predict future inflation and add a risk premium based on that prediction. The study will be updated in the coming weeks using the 14-country data set.
technical details
The daily government bond yields of the above 14 countries form the basic historical data for the number of factors and their volatility in the fitted yield curve. Bund historical information provided by Deutsche Bundesbank. The use of the international bond data increases the number of observations to more than 106,000 and provides a more complete experience of high and negative interest rates than using the Bund data set alone.
The modeling process was published in very important paper By David Heath, Robert Jarrow and Andrew Morton, 1992:
Econometrics
The arbitrage-free foreign exchange rate simulation is based on this famous paper by Amin and Jarrow:
international journal of money and finance
For technically inclined readers, we recommend Professor Jarrow’s book Modeling fixed income securities and interest rate options For those who want to know exactly how the “HJM” model is built.
The number of factors for the 14-country model is 12, which has remained stable for some time.
Footnote:
(1) After the first 20 years of the simulation, the 10-year yield cannot be derived from the original 30-year yield structure.
(2) The actual simulation used a time step of 91 days, spanning a time horizon of 30 years.
Editor’s note: This article covers one or more micro-cap stocks. Please be aware of the risks associated with these stocks.






